Lösung von ordinalen Optimierungsprobleme mittels multikriterieller Optimierung
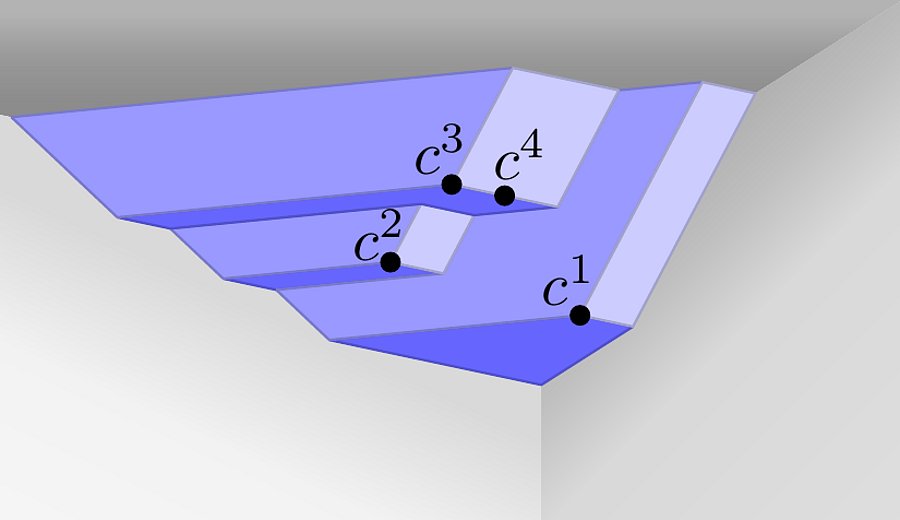
Ordinale Optimierungsprobleme betrachten geordnete Kategorien (wie gut, mittel, schlecht) statt reeller Kostenkoeffizienten. Es wird der Bezug zwischen verschiedenen Optimalitätskonzepten für ordinale Kosten und die bijektive, lineare Transformation von ordinalen Kosten zu multikriteriellen Kosten analysiert. Damit ist es möglich Optimierungsprobleme mit ordinalen Kosten mit bekannten Methoden für multikriterielle Optimierung zu lösen.
Der Artikel ist unter folgendem Link abrufbar: https://authors.elsevier.com/a/1h7Q61LnJ6pHe7
zuletzt bearbeitet am: 28.06.2023
